Notes for Prof. Hung-Yi Lee's ML Lecture: Self-Attention
Self-Attention
With a vector sequence as input, self-attention can produce a sequence of vectors (or scalars) of the same length. The produced vectors can then be fed into feedforward networks or further self-attention layers. Conceptually, the production of every vector takes into account the whole input sequence, evaluate some parts as more relevant and let the relevant ones contribute more.
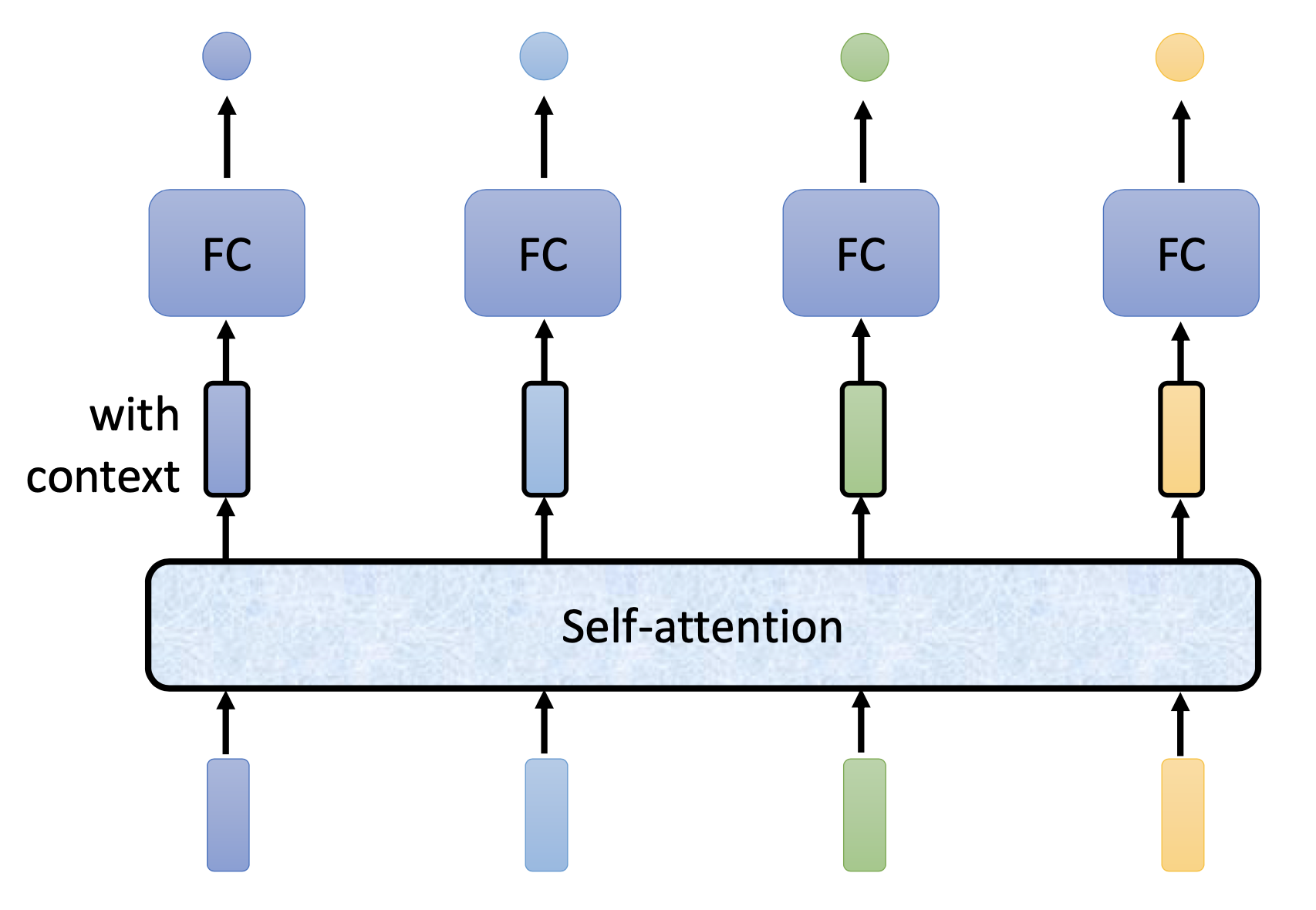
Operations
For a sequence of $n_i$ vectors as input, for every vector $a_{i}$, we calculate the relevance $\alpha_{j}$ to every vector $a_j$. We also produce a value vector $v_j$ for every vector $a_j$. Then we calculate a weighted sum over $v_j$’s by $\alpha_{j}$’s as the output $b_i$ for vector $a_i$. After calculating $b_i$’s for all the input vectors, we operations of a self-attention layer is done.
The detailed operations:
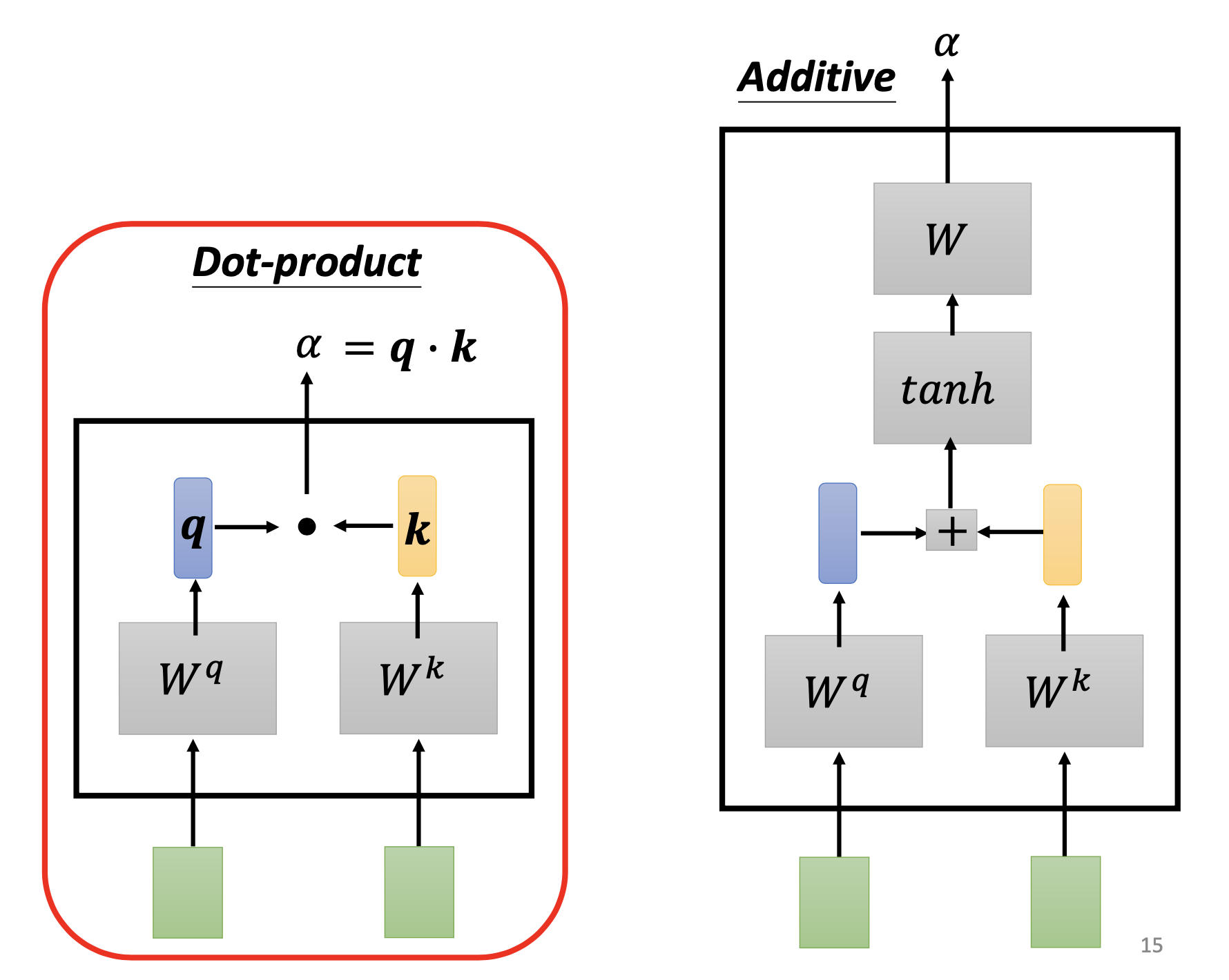
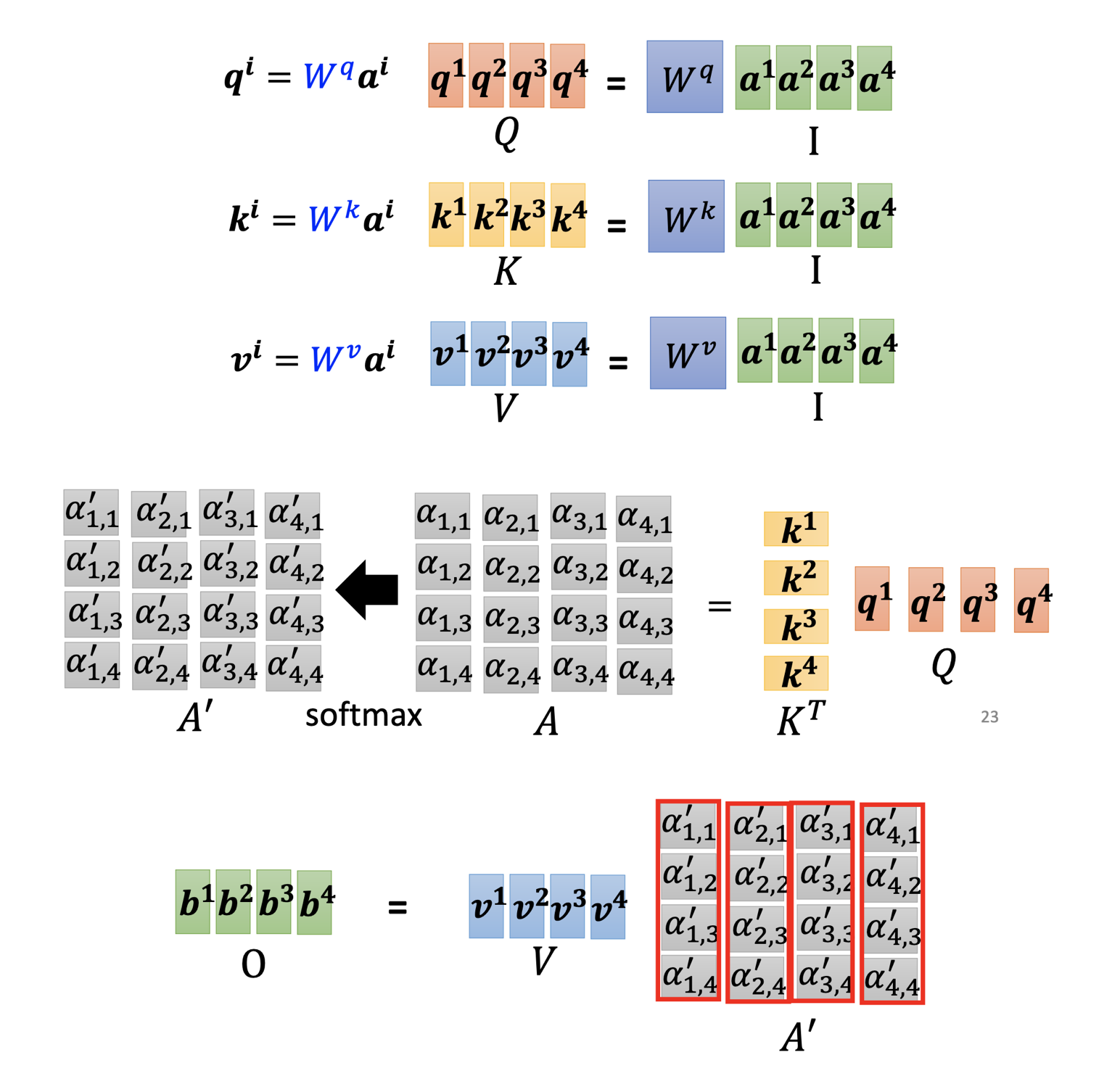
For every input vector $a_i$, we multiply it by the query matrix $W^q$ to produce a query vector $q_i$. Then for every input vector $a_i$, we multiply it by matrix $W^k$ to produce a key vector $k_i$.
Then we calculate the scalar relevance $\alpha_{j}$ for every vector $a_j$ to vector $a_i$ by dot product or other computations:
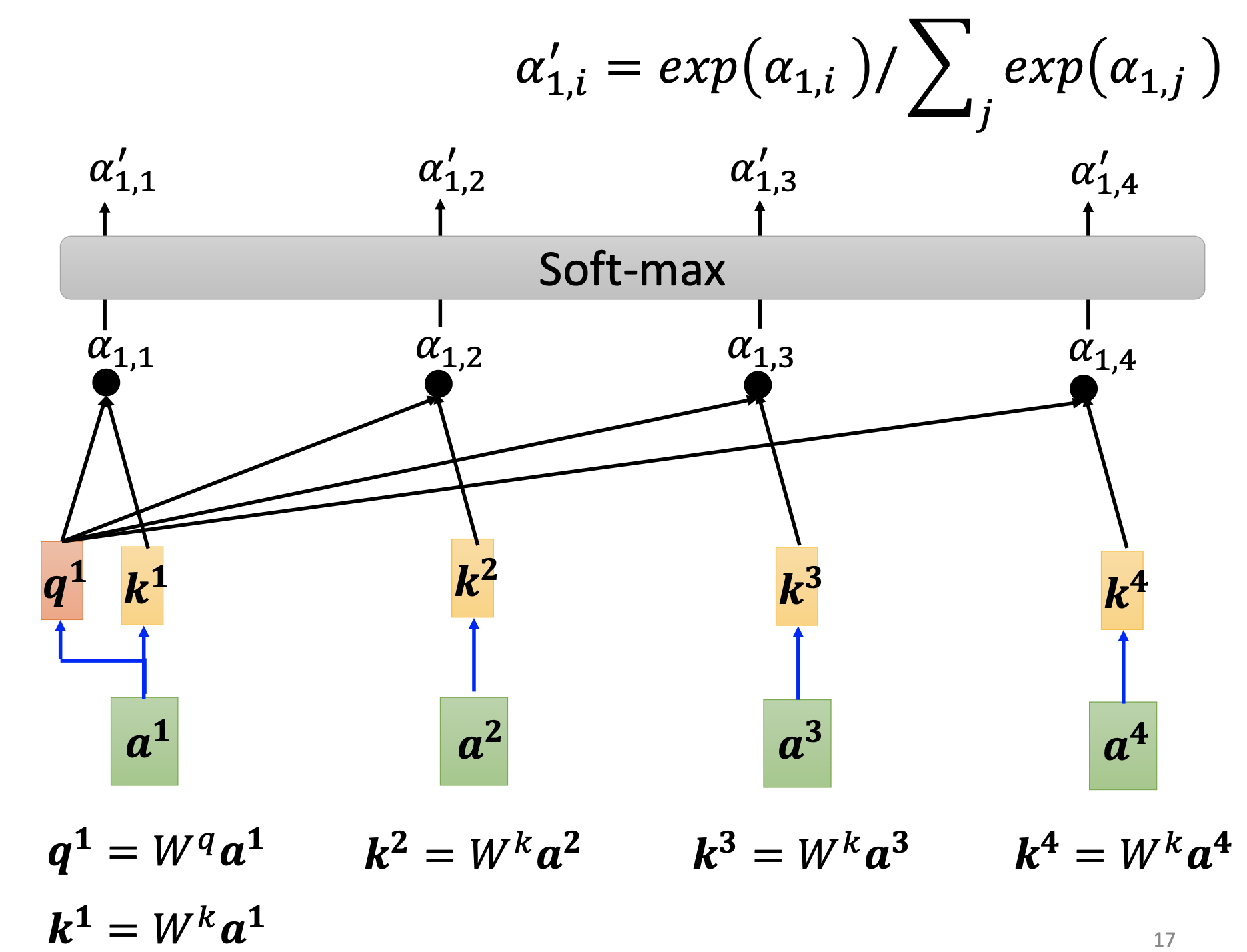
Then we use softmax to normalize the $\alpha_{j}$’s to get the $\alpha’_{j}’s$. We can also use other non-linear functions instead of softmax.
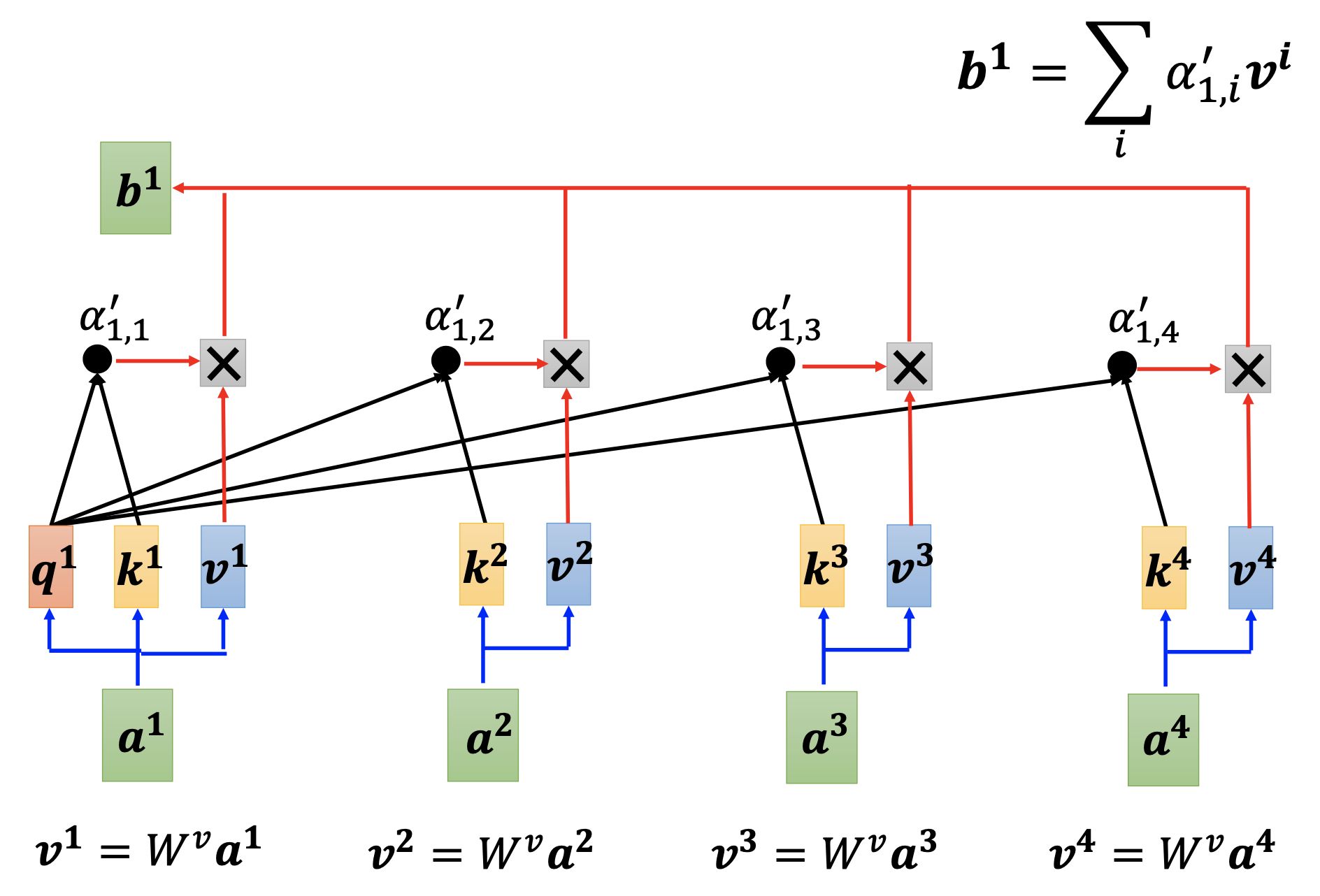
Then we produce a value vector $v_j$ for every vector $a_j$ by matrix $W^v$. Then we use the $\alpha_{j}$’s as weights to sum the $v_j$’s to get the output vector $b_i$ for $a_i$. By repeating these procedures for all the $a_i$’s, we get the output vectors $b_i$’s for the input sequence $a_i$’s.
Dimensions of the vectors and matrices:
- $a$: $n_a$ dimentions.
- $q$: $n_{\alpha}$ dimensions.
- $W^q$: $n_{\alpha} \times n_{a}$ dimensions.
- $k$: $n_{\alpha}$ dimensions.
- $W^k$: $n_{\alpha} \times n_{a}$ dimensions.
- $v$: $n_b$ dimensions.
- $W^v$: $n_{b} \times n_{a}$ dimensions.
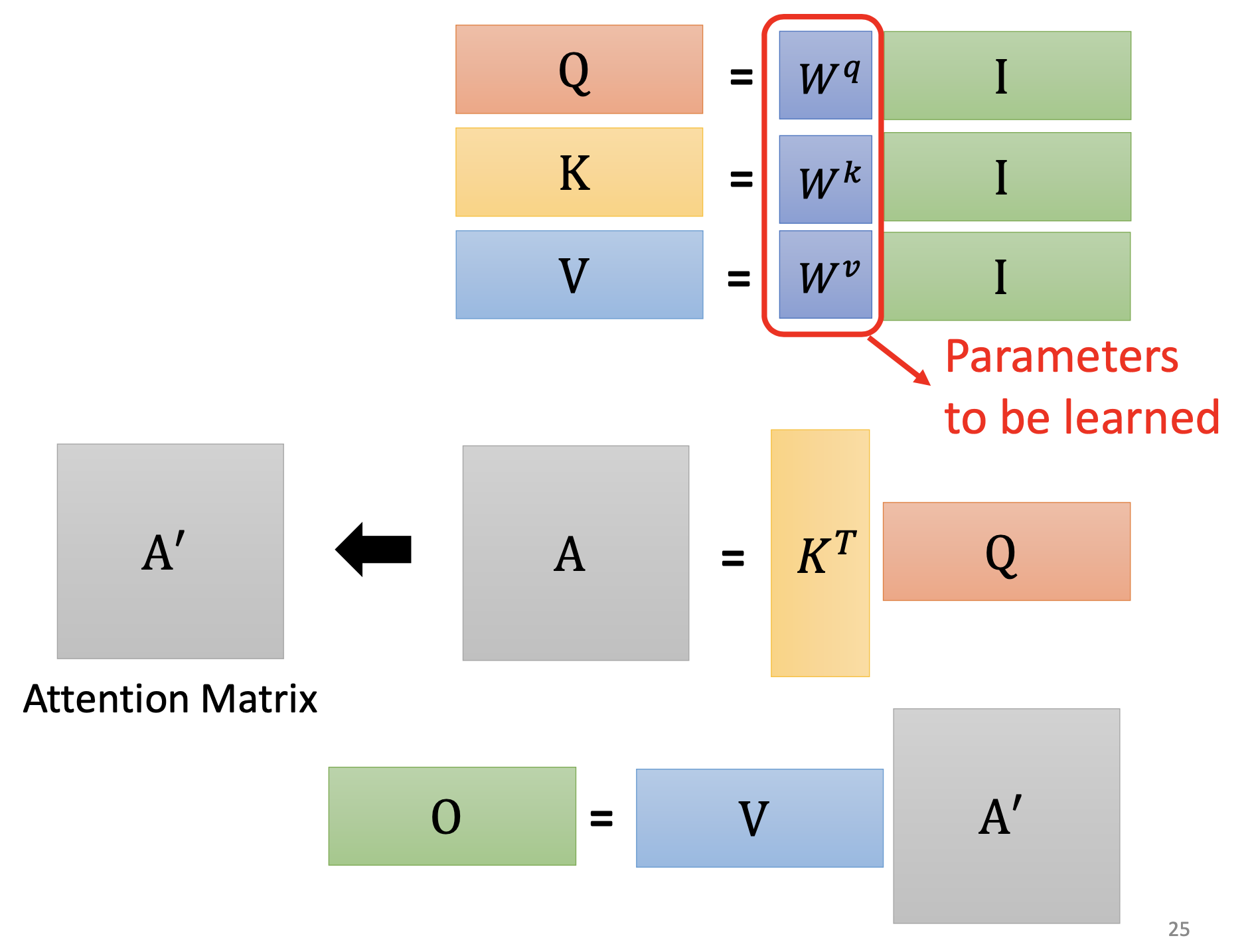
Operations as Matrices Computation
The operations over individual $a_i$’s to produce $b_i$’s can be composed as matrices computations:
Multi-Head Self-Attention
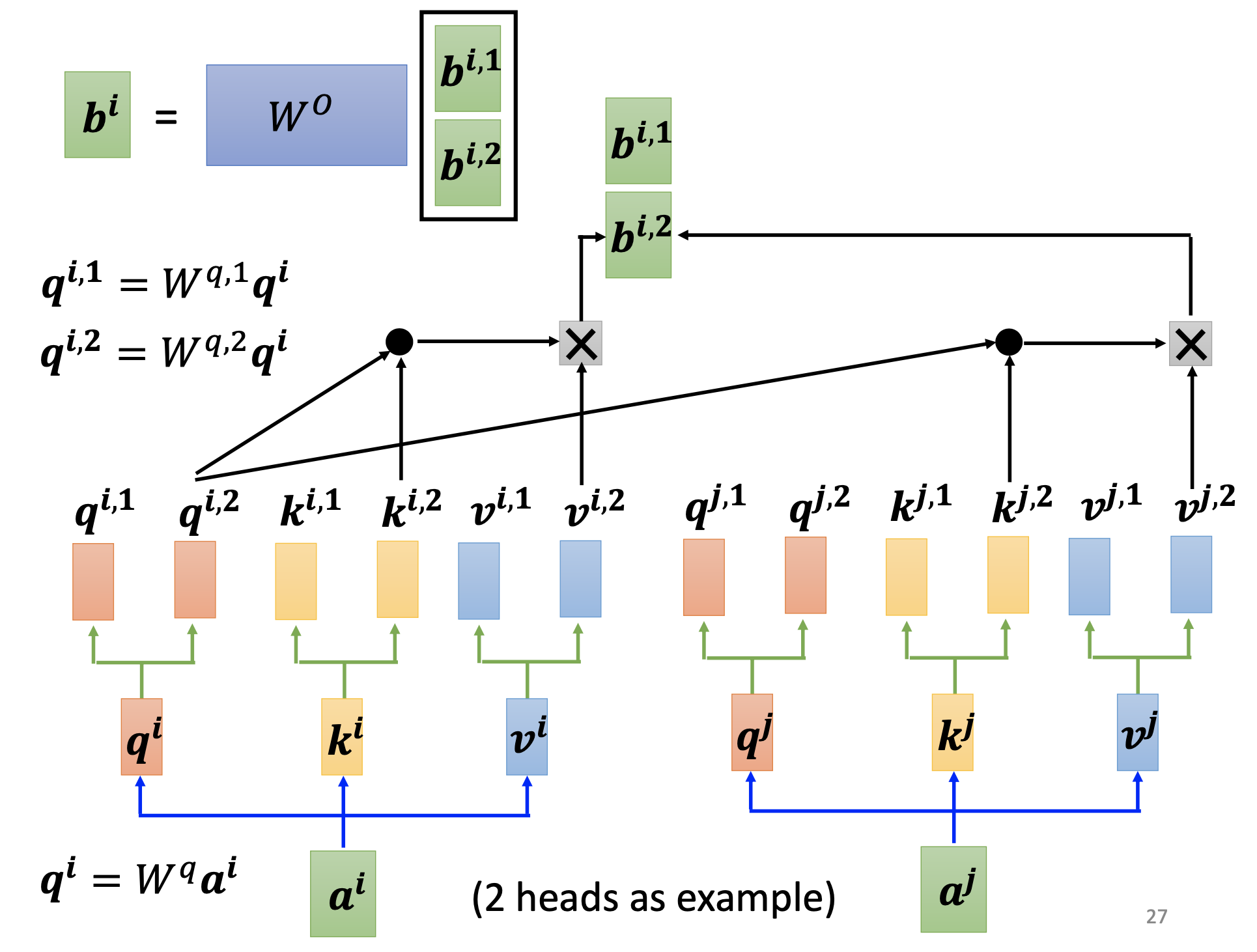
We may need more than a single attention mechanisms at a time, i.e. different type of relevances.
For multi-head attention, we multiply $q_i$’s, $k_i$’s and $v_i$’s by additional matrices $W^{q,t}$, $W^{k,t}$, $W^{v,t}$ to produce $q^t_i$’s, $k^t_i$’s and $v^t_i$’s to get $b^t_i$’s. We then concatenate the $b^t_i$’s and multiply it by $W^o$ to get the final output $b_i$.
Positional Encoding
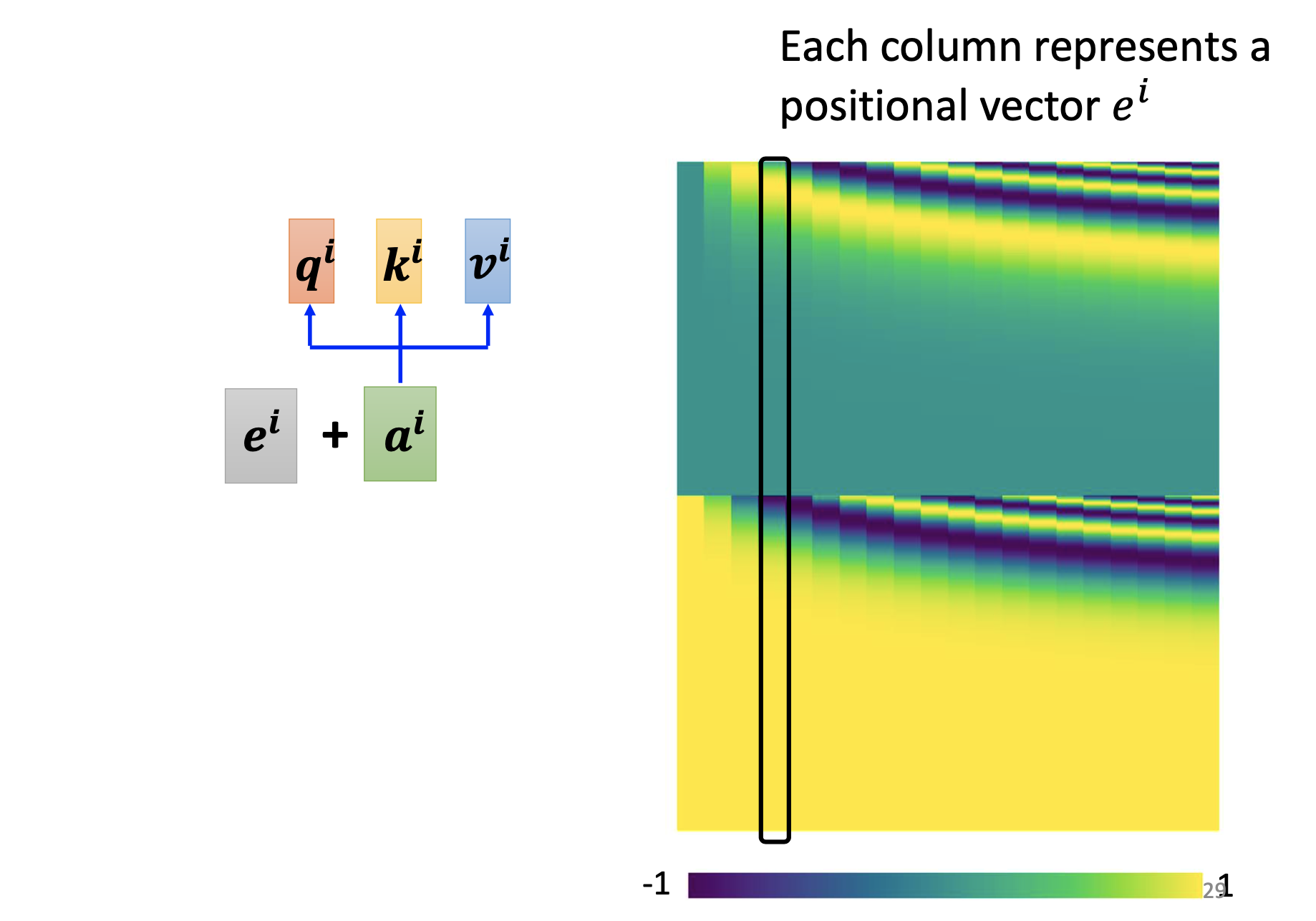
By the procedures explained so far, the information of positions are not included. To take into account them, we add a vector $e_i$ to every $a_i$ with respect to its position. Which kind of encoding is better is still an open question.
Comparing with other Networks
Self-Attention vs CNN
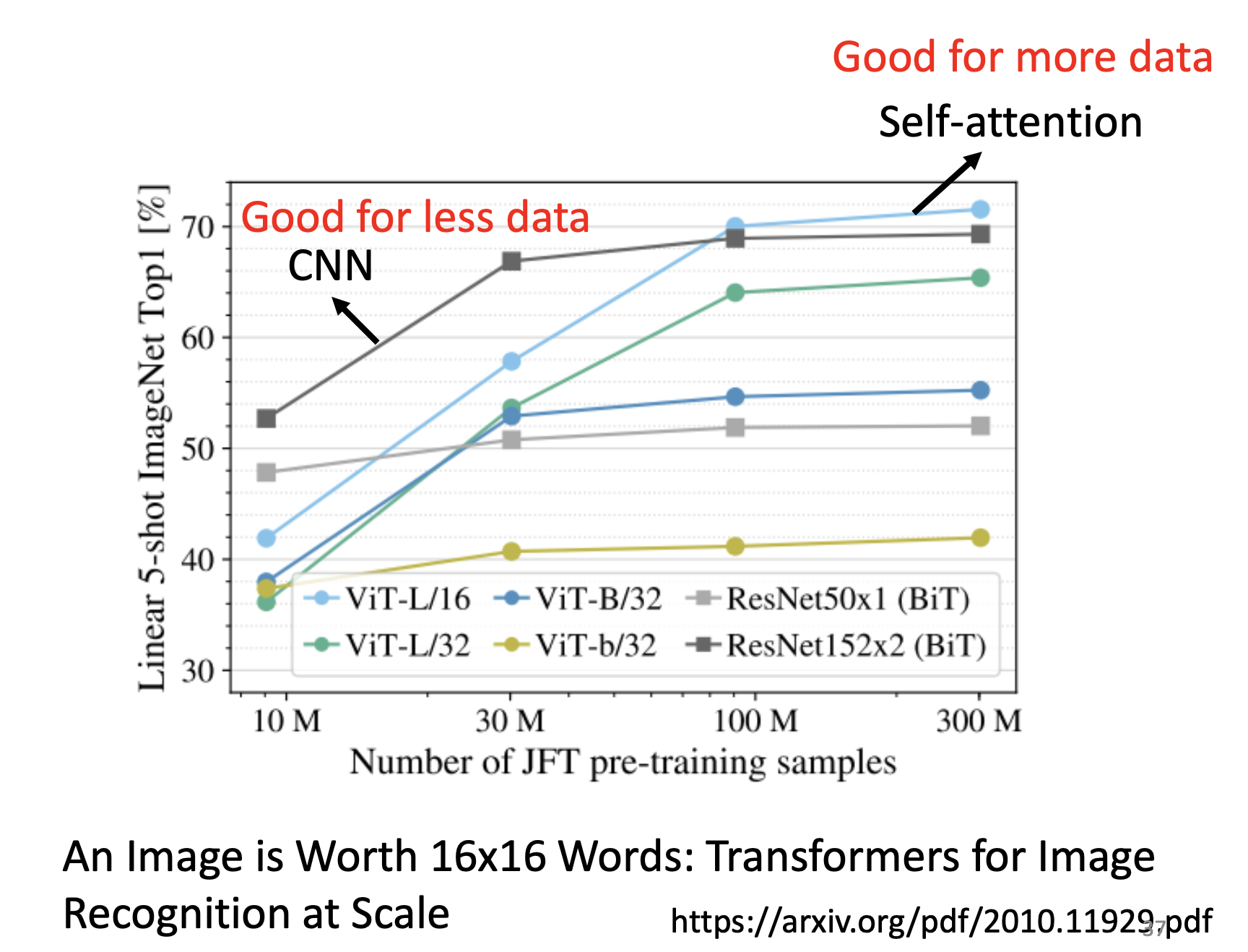
CNN is self-attention that can only attend in a receptive field. Self-attention is CNN with learnable receptive field. Self attention is a larger function set that contains CNN. Therefore, with fewer data, CNN may outperform self-attention due to less overfitting; with more data, self-attention may outperform CNN by stronger fitting power.
Self-Attention vs RNN
In general, self-attention outperforms RNN because RNN is limited by its memoery capacity over long sequences, while self-attention can attend to every position in the sequence parallelly.
References
Youtube: 【機器學習2021】自注意力機制 (Self-attention) (上)