Notes for Prof. Hung-Yi Lee's ML Lecture: Support Vector Machine
My Intuitive Explanation
The overall computation is equivalent to:
- transform the features to a high-dimensional (often infinite-dimensional) space.
- find a plane to separate the 2 classes by the hinge loss.
- use the plane to classify new data.
with the tricks:
- By the kernel method, when classifying new data, we calculate the kernel function betwen the new data and all the training data in the original space, so we don’t have to perform computations in the high-dimensional space.
- By the kernal method and the hinge loss, we only have to calculate the kernel product between the new data and only a few data points of the training set near the classification boundary. These training data points are the support vectors.
Traditional Formulation
I refer to Bishop Chap.7.1 for this part.
For Separable Class Distributions
Defining the Problem
For a binary classificaiton problem, we have the function:
\[y(x) = w^{T} \phi(x) + b \text{, } t_{n} = \begin{cases} 1 & \text{ when } y(x) > 0 \\ -1 & \text{ when } y(x) < 0 \end{cases}\]We assume the data to be perfectly separable, then
\[t_{n} y(x_{n}) > 0\]To find the plane with maximum margin, we try to find $w, b$ by
\[arg \max\limits_{w, b} \{\frac{1}{\| w \|} \min\limits_{n} [t_{n} (w^{T}\phi(x_{n}) + b)] \}\]
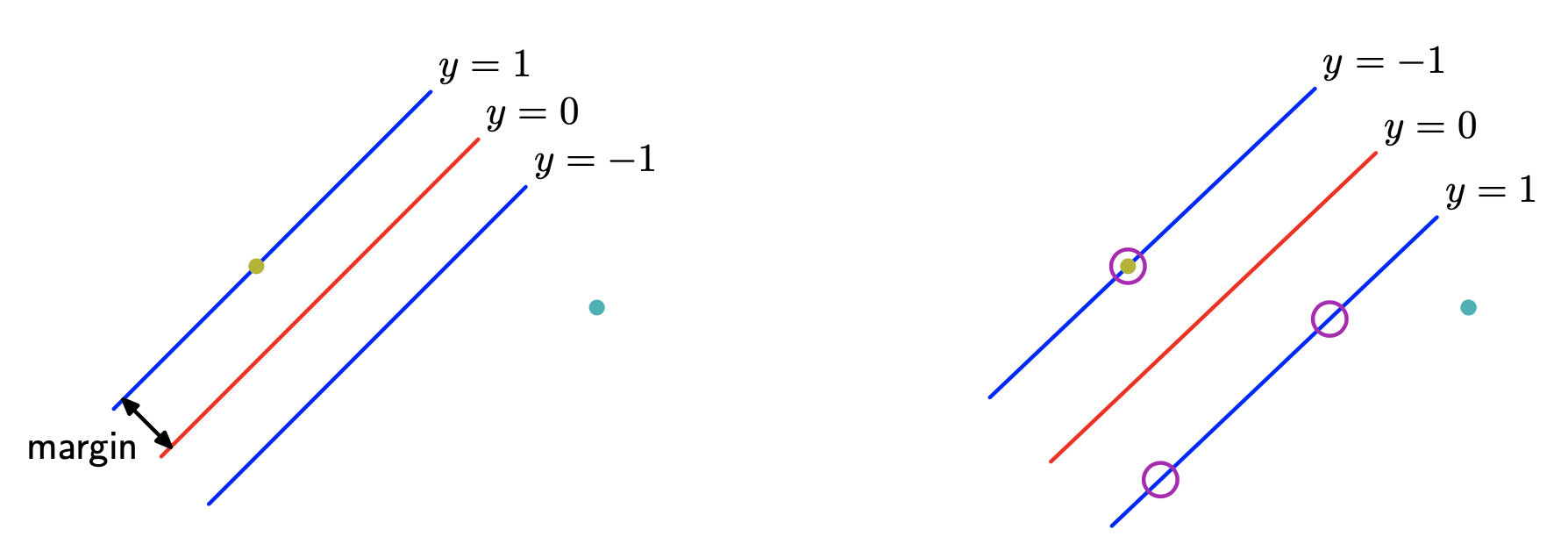
Derivations
By $w \to \kappa w$ and $b \to \kappa b$, for the points that are closest to the boundary, we can set
\[t_{n} (w^{T}\phi(x_{n}) + b) = 1\]then for all points,
\[t_{n} (w^{T}\phi(x_{n}) + b) \geq 1\text{, } n = 1, \dotsc, N\]Then the questions is equivalent to
\[arg \min\limits_{w, b} \frac{1}{2} \| w \|^2\]with constraints
\[t_{n} (w^{T}\phi(x_{n}) + b) \geq 1\text{, } n = 1, \dotsc, N\]Then by Lagrange multiplier, we get the Lagrangian
\[L(w,b,a) = \frac{1}{2} \| w \|^2 - \sum_{n=1}^{N} a_n \{ t_{n} (w^{T}\phi(x_{n}) + b) - 1 \} \\ a_n \geq 0 \text{, } a = (a_1, \dotsc, a_N)^T\]By optimizing $w$ & $b$ by $0$ gradient, we get
\[w = \sum_{n=1}^{N} a_n t_n \phi(x_n) \\ 0 = \sum_{n=1}^{N} a_n t_n\]then we get the dual representation:
\[\tilde{L} (a) = \sum_{n=1}^{N} a_n - \frac{1}{2} \sum_{n=1}^{N} \sum_{m=1}^{N} a_n a_m t_n t_m k(x_n, x_m)\]which subject to
\[a_n \geq 0 \text{, } \sum_{n=1}^{N} a_n t_n = 0\]where $k(x, x’) = \phi^T(x)\phi(x’)$ is the kernel function. Also, by the Lagrange multiplier, the KKT conditions are
\[a_n \geq 0 \\ t_n y(x_n) - 1 \geq 0 \\ a_n \{ t_n y(x_n) - 1 \} = 0\]Now it became a quadratic programming problem that we can solve by the established approaches to find the $a$’s.
Inference
\[y(x) = \sum_{n=1}^{N} a_n t_n k(x, x_n) + b \text{, } t_{n} = \begin{cases} 1 & \text{ when } y(x) > 0 \\ -1 & \text{ when } y(x) < 0 \end{cases}\]Discussions on the Support Vectors
By the KKT conditions, when $a_n = 0$, then $x_n$ is behind the correct margin and is not a support vector; when $a_n > 0$, then $x_n$ is on the margin and is a support vector.
Alternative Formulation
We can express the maximum-margin classifier in terms of the minimization of an error function, with a simple quadratic regularizer, in the form
\[\sum_{n=1}^{N} E_{\infty} (y(x_n)t_n - 1) + \lambda \| w\|^2\]where $E_{\infty}(z)$ is a function that is $0$ if $z \geq 0$ and $\infty$ otherwise. Note that as long as the regularization parameter satisfies $\lambda > 0$, its precise value plays no role.
For Overlapping Class Distributions
Defining the problem
For a binary classificaiton problem, we have the function:
\[y(x) = w^{T} \phi(x) + b \text{, } t_{n} = \begin{cases} 1 & \text{ when } y(x) > 0 \\ -1 & \text{ when } y(x) < 0 \end{cases}\]To have a “soft margin”, i.e. to allow the data points to be on the wrong side, we introduce the slack variables $\xi_n \geq 0$, $n = 1, \dotsc, N$ for each training data point. $\xi_n = 0$ for data points on or inside the correct margin boundary and $\xi_n = \vert t_n - y(x_n) \vert$ otherwise.
To find the plane with maximum margin, we try to find $w, b$ by
\[arg \max\limits_{w, b} \{\frac{1}{\| w \|} \min\limits_{n} [t_{n} (w^{T}\phi(x_{n}) + b)] \}\]
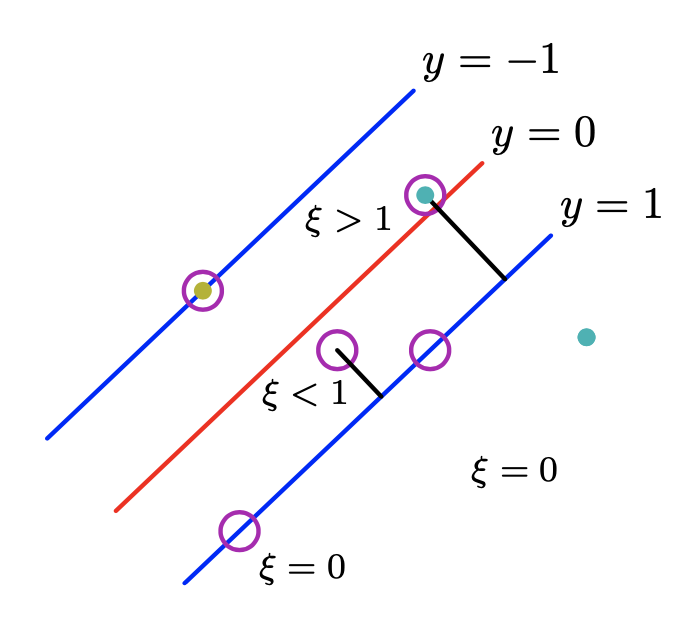
Derivation
By $w \to \kappa w$ and $b \to \kappa b$, for the points that are on the correct boundary, we can set
\[t_{n} (w^{T}\phi(x_{n}) + b) = 1\]then for all points,
\[t_{n} (w^{T}\phi(x_{n}) + b) \geq 1 - \xi_n \text{, } n = 1, \dotsc, N\]then the question is equivalent to
\[arg \min\limits_{w, b} ( C \sum_{n=1}^{N} \xi_n + \frac{1}{2} \| w \|^2 )\]with constraints
\[t_{n} (w^{T}\phi(x_{n}) + b) \geq 1 - \xi_n \text{, } n = 1, \dotsc, N\]where $C > 0$. And when $C \to \infty$, it became the SVM for separable data.
Then by Lagrange multiplier,
\[L(w, b, a) = \frac{1}{2} \| w \| ^2 + C \sum_{n=1}^{N} \xi_n - \sum_{n=1}^{N} a_n \{ t_n y(x_n) - 1 + \xi_n \} - \sum_{n=1}^{N} \mu_n \xi_n\]and we get the KKT conditions:
\[a_n \geq 0 \text{, } \mu_n \geq 0 \text{,} \\ t_n y(x_n) - 1 + \xi_n \geq 0 \text{, } \xi_n \geq 0 \text{,} \\ a_n (t_n y(x_n) - 1 + \xi_n) = 0 \text{, } \mu_n \xi_n = 0 \text{.}\]To optimize $w$, $b$, ${ \xi }$,
\[\frac{\partial L}{\partial w} = 0 \Rightarrow w = \sum_{n=1}^{N} a_n t_n \phi(x_n) \\ \frac{\partial L}{\partial b} = 0 \Rightarrow \sum_{n=1}^{N} a_n t_n = 0 \\ \frac{\partial L}{\partial \xi_n} = 0 \Rightarrow a_n = C - \mu_n \\\]then
\[\tilde{L} (a) = \sum_{n=1}^{N} a_n - \frac{1}{2} \sum_{n=1}^{N} \sum_{m=1}^{N} a_n a_m t_n t_m k(x_n, x_m)\]The $\tilde{L}$ is the same as the separable data SVM. And it subject to
\[0 \leq a_n \leq C \text{(the }\textit{box constraint}\text{), } \sum_{n=1}^{N} a_n t_n = 0\]then it became a quadratic programming problem that can be solved by the established approaches.
Inference
Identical to the separable data SVM,
\[y(x) = \sum_{n=1}^{N} a_n t_n k(x, x_n) + b \text{, } t_{n} = \begin{cases} 1 & \text{ when } y(x) > 0 \\ -1 & \text{ when } y(x) < 0 \end{cases}\]Discussions on Support Vectors
For the training data points,
| Condition | Location | Is Suppport Vector? |
|---|---|---|
| $a_n = 0$ | inside the correct margin | N |
| $C > a_n > 0$ | on the margin | Y |
| $C = a$ | out of the correct margin | Y |
Alternative Formulation
\[\sum_{n=1}^{N} \max (1 - y(x_n)t_n, 0) + \lambda \| w\|^2\]where the former term is the Hinge loss.
Binary Classifier
Multiclass SVM
Although the application of SVMs to multiclass classification problems remains an open issue, in practice the one-versus-the-rest approach is the most widely used in spite of its ad-hoc formula- tion and its practical limitations.
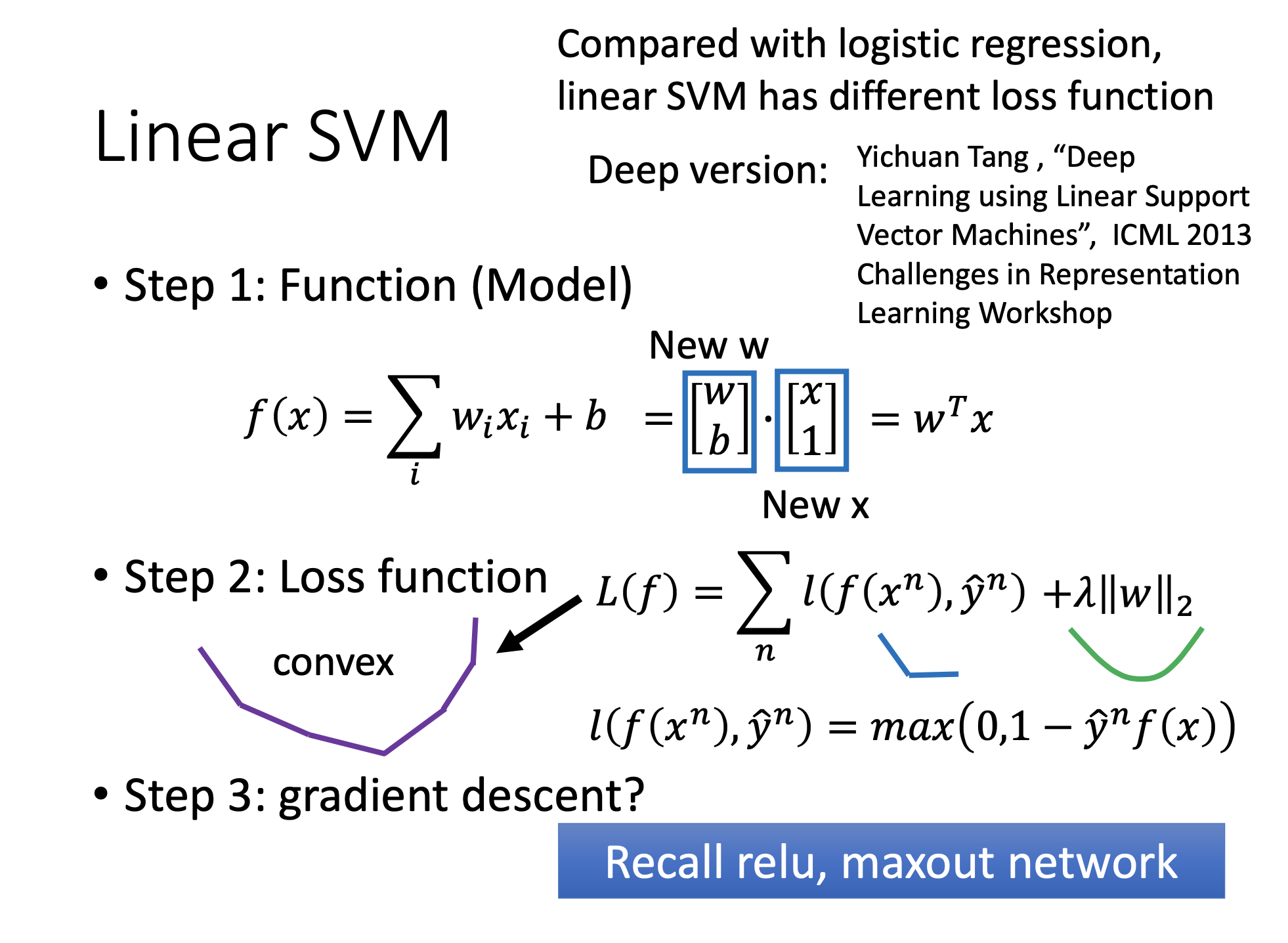
Prof. Lee’s Formulation by the 3 Steps of ML
References
Youtube ML Lecture 20: Support Vector Machine (SVM)
Pattern Recognition and Machine Learning, Christopher M. Bishop, 2006