Notes for Prof. Hung-Yi Lee's ML Lecture 10: CNN
CNN: Convolutional Neural Networks
When using fully connected networks on images, the number of parameters may be too large. By applying constraints on the networks based on properties of images, we can reduce the total number of parameters.
The fundamental concept of CNN is “to let filters convolve through the image”.
Input Images
The color images have 3 channels (RGB) on every pixel; the black-white have only 1 channel.
We have to transform the input image to the size of the input of the network in advance.
Scaling and rotation of the image training data impact the training results of CNN, i.e. The trained CNN is not invariant for scaling and rotation. However, a proper image recognizer should be able to generate the same output by input images with scaling or rotation. Therefore, we have to generate more training data by performing scaling and rotation on the training images, i.e. performing data augmentation.
Properties of Images & the CNN Techniques
When using the CNN techniques, make sure that your task meet the corresponding properties. For example AlphaGo don’t use pooling; NLP/Speech recognition only convolve through a single dimension (word sequence / frequency). In NLP, the vectors on the other dimension are not spatially related to the neighboring ones (word vector dimentions ); in speech recognition, the shift-invariant effect on the dimention of time is handled by recurrentness of the network.
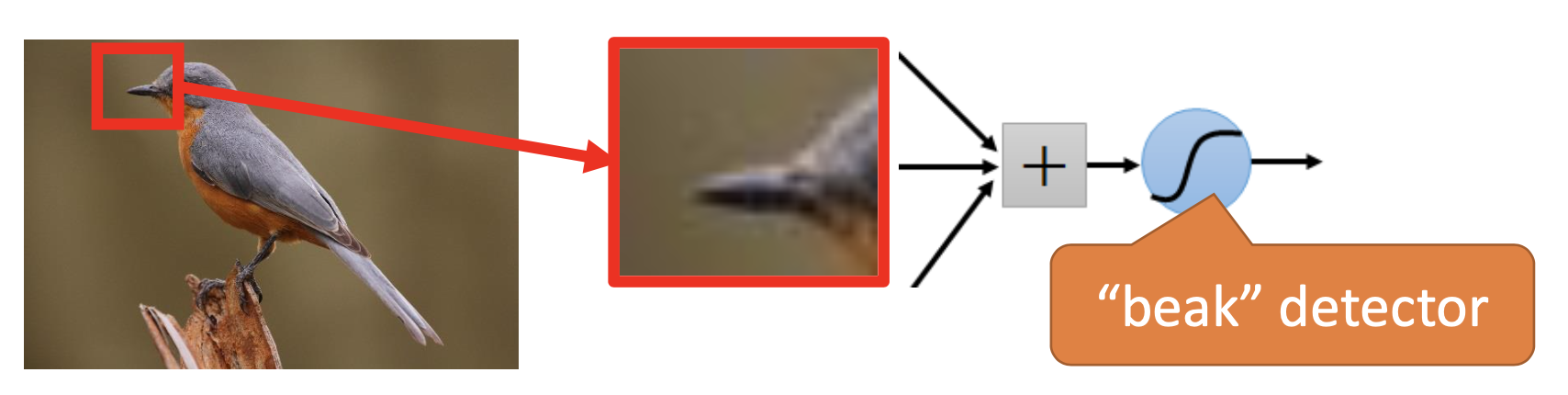
Critical Patterns in Small Areas: Filters
In images, the critical patterns for recognition are usually in areas that are smaller than the whole image or even in small regions, so we use filters to find the patterns. The area that a filter processes is the receptive field.
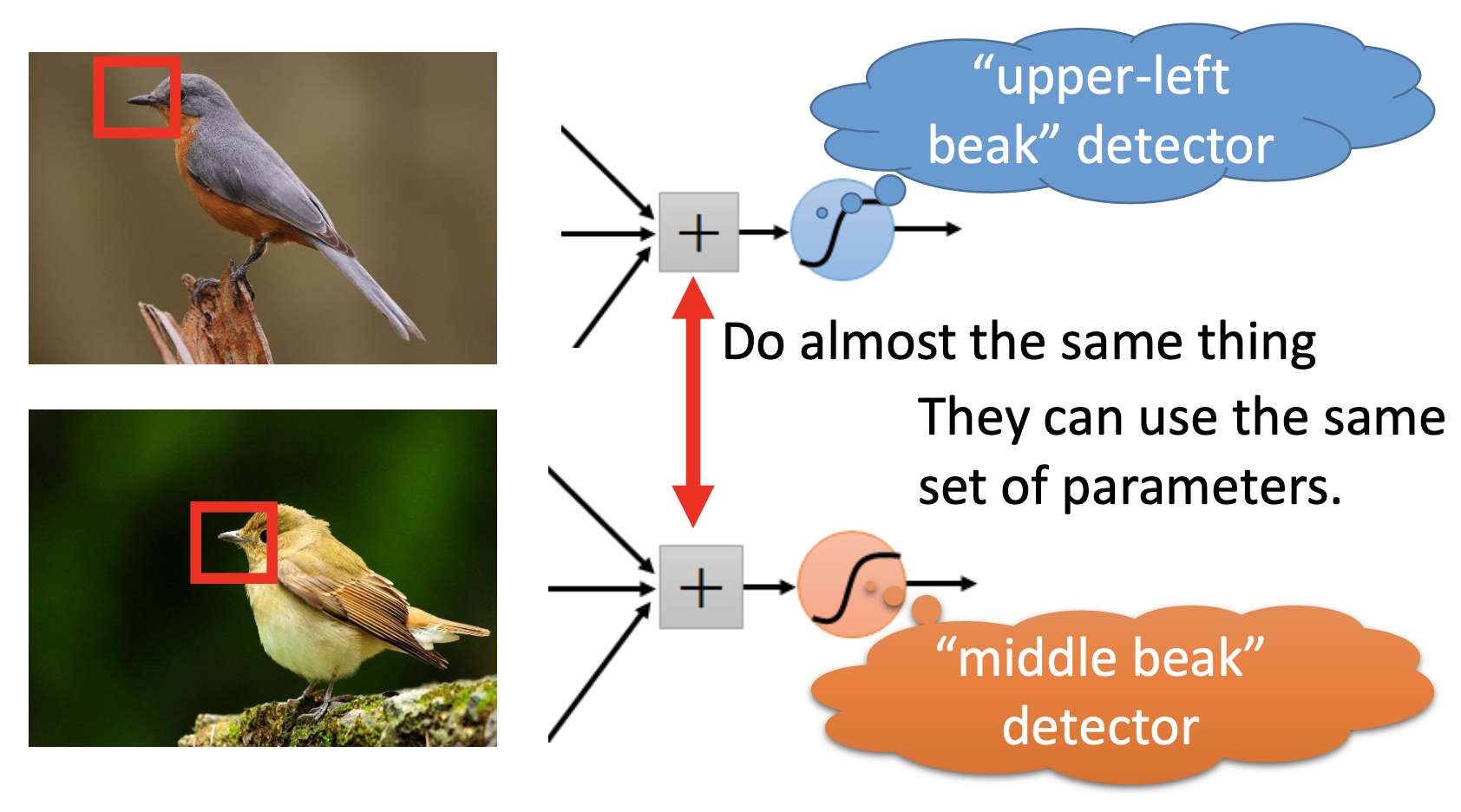
Critical Patterns at Different Regions: Weight Sharing
In images, the critical patterns may appear in different regions of the images, so the filters for the same pattern at different locations should share their weights.
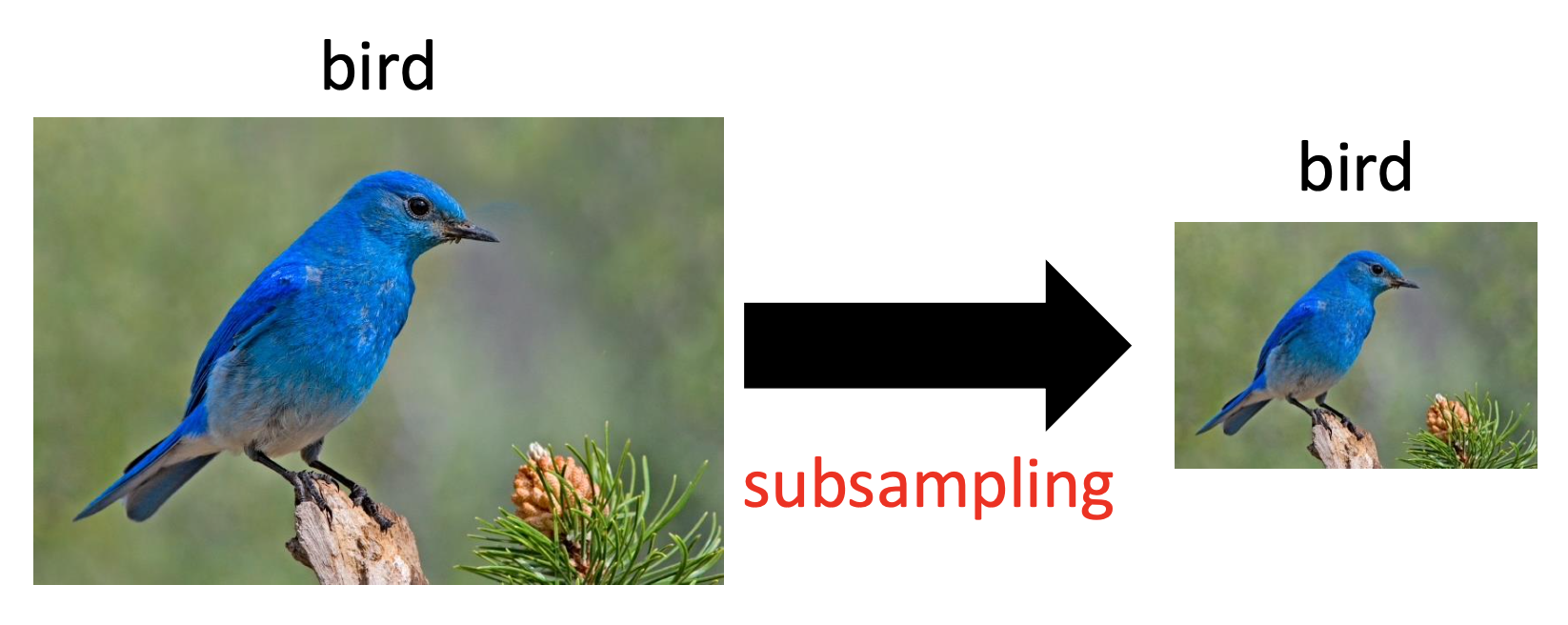
Subsampling Don’t Impact the Recognition: Pooling
Subsampling of the image don’t change the object, so we can apply pooling to further reduce the total number of parameters.
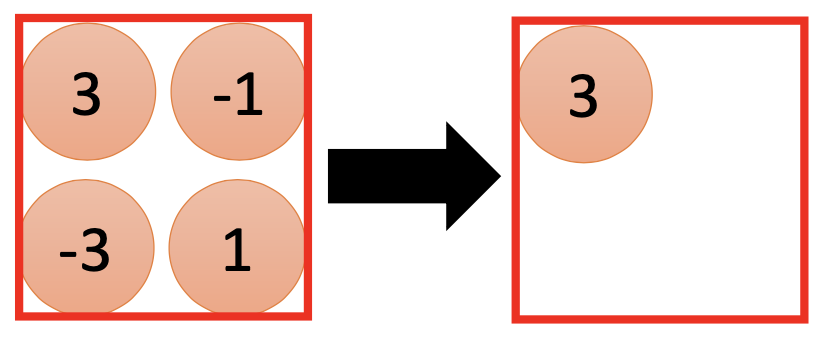
And example of pooling:
Recently some networks don’t use pooling because the computing cost is not too high for their computing power.
CNN Structure
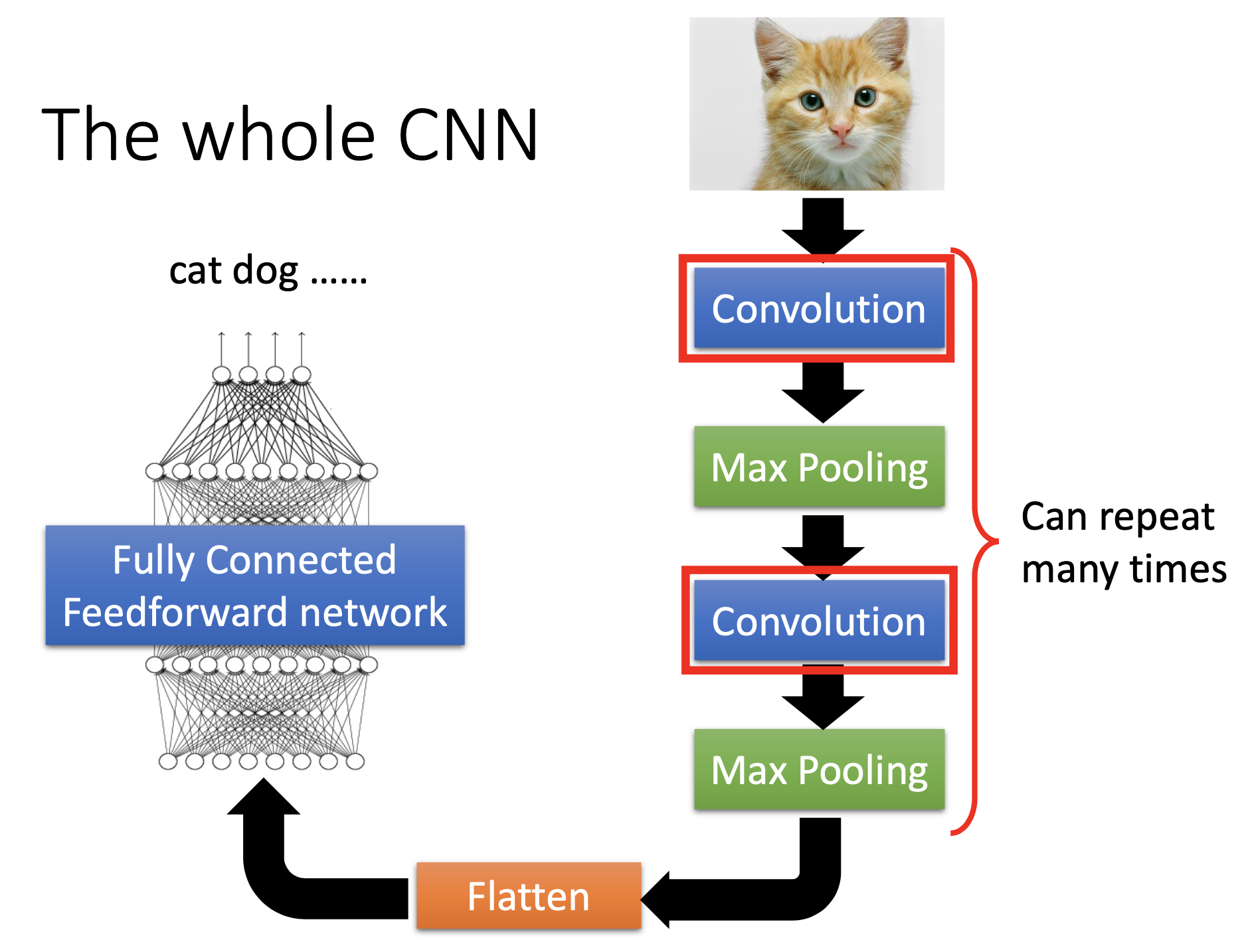
Total Number of Neurons & Connections for a Convolution Layer
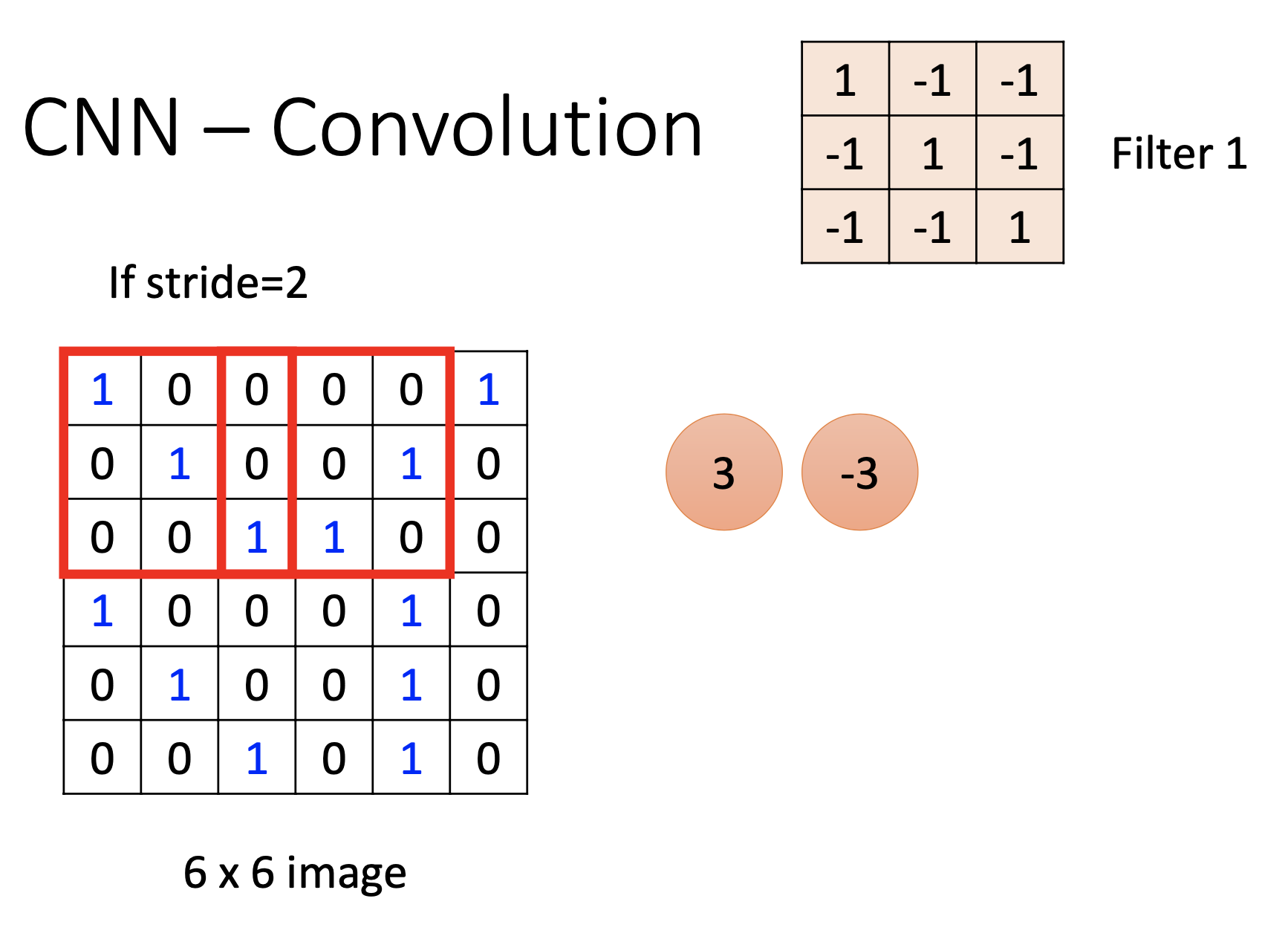
Stride: the pixel distance between the neighboring receptive filds.
Padding: when using padding, if a receptive field at the edge exceeds the edge, then the exceeding part will be filled based on the padding method. Usually we use 0 padding, i.e. pad with 0’s.
Feature map: The output map produced by applying a filter over the input / pre-layer output.
Assume the shape of input and output are squares. Total number of weights of the convolution layer:
\[n_f (n_{rs})^2 n_{ch}\]where $n_f$ is the total number of filters, $n_{rs}$ is the size of one side of the receptive field, $n_{ch}$ is the total number of channels of the input.
The total number of output neurons:
\[(\frac{n_{in} - n_{rs} + 1}{n_s} \text{ round up})^2 n_f\]where $n_s$ is stride, $n_{in}$ is the size of a side of the input.
Gradient Descent on Input
To see the pattern that a neuron in a CNN learns to recognize, we can perform gradient descent on the input image to maximize the activation of the neuron.
By the example of digit recognition, we can also see that some non-sense input are going to be recognized as digits => deep neural networks are easily fooled (see link).
Similar technique can also be used for Deep Dream and Deep Style.
Deep Dream
Let an CNN show what it sees in an image.
Steps:
- Run the CNN on an image
- choose a layer and exaggerate the values
- perform gradient descent on the input image to let the layer geach the exaggerated values.