Notes for Prof. Hung-Yi Lee's ML Lecture 7: Backpropagation
For applying gradient descent on neural networks, there may be millions or more parameters, and we use backpropagation to compute the gradients efficiently.
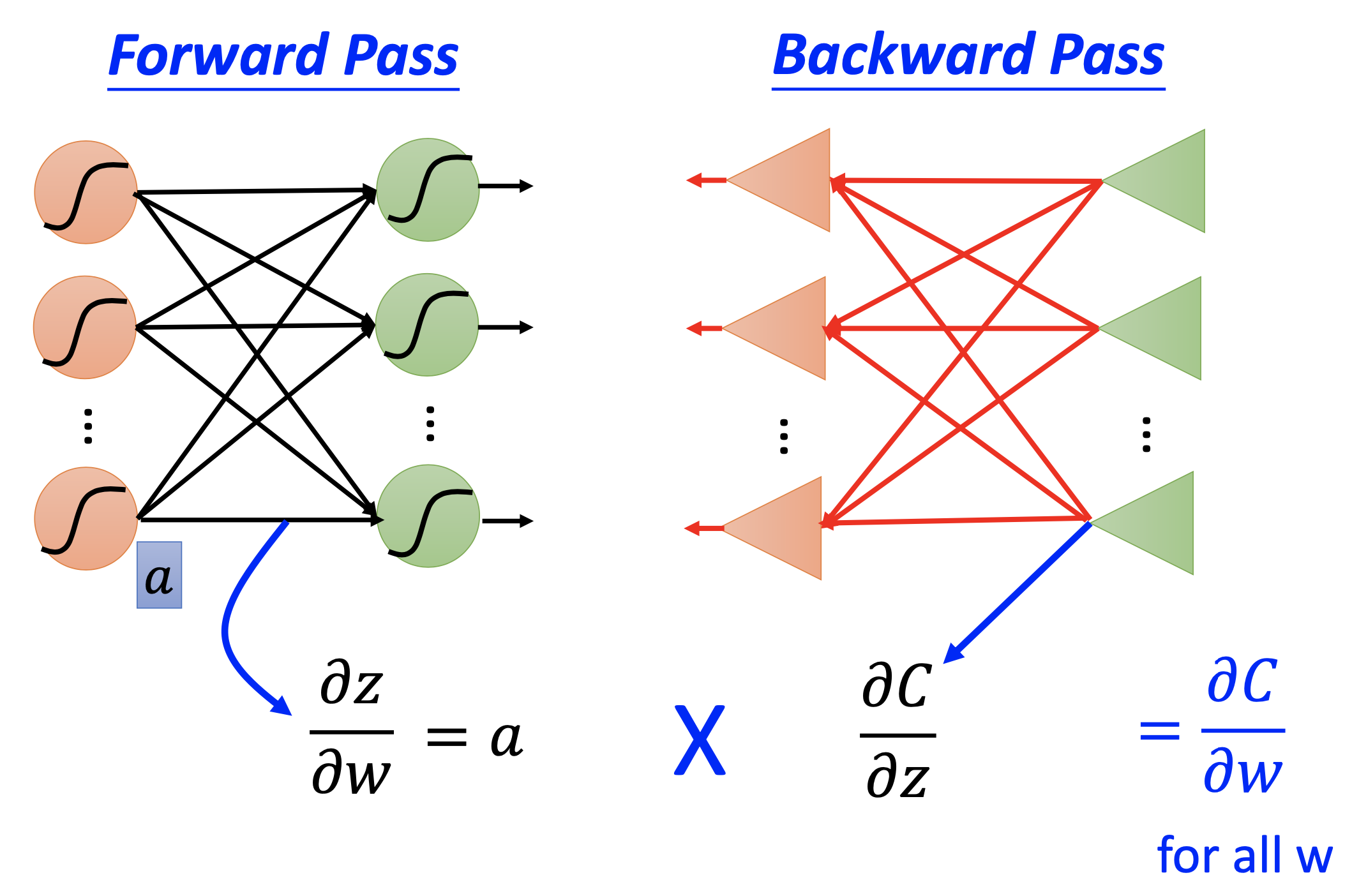
Forward Pass
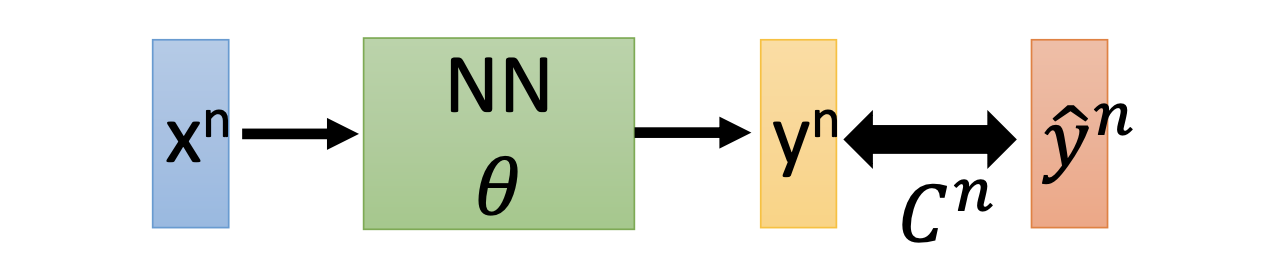
For an NN with $\theta$ as the vector that represent all the parameters and $L(\theta)$ as the loss function, $L(\theta) = \sum_{n=1}^{N} C^n (\theta)$, and
\[\frac{\partial L(\theta)}{\partial w_i} = \sum_{n=1}^{N} \frac{\partial c^n (\theta)}{\partial w_i}\]Then for any example $n$ and parameter $i$,
\[\frac{\partial C^n}{\partial w_i} = \frac{\partial z_p}{\partial w_i} \frac{\partial C^n}{\partial z}\]where $z_p$ is the total input at the node of $w_i$ and $z_p = x_i w_i + \dots$, for example
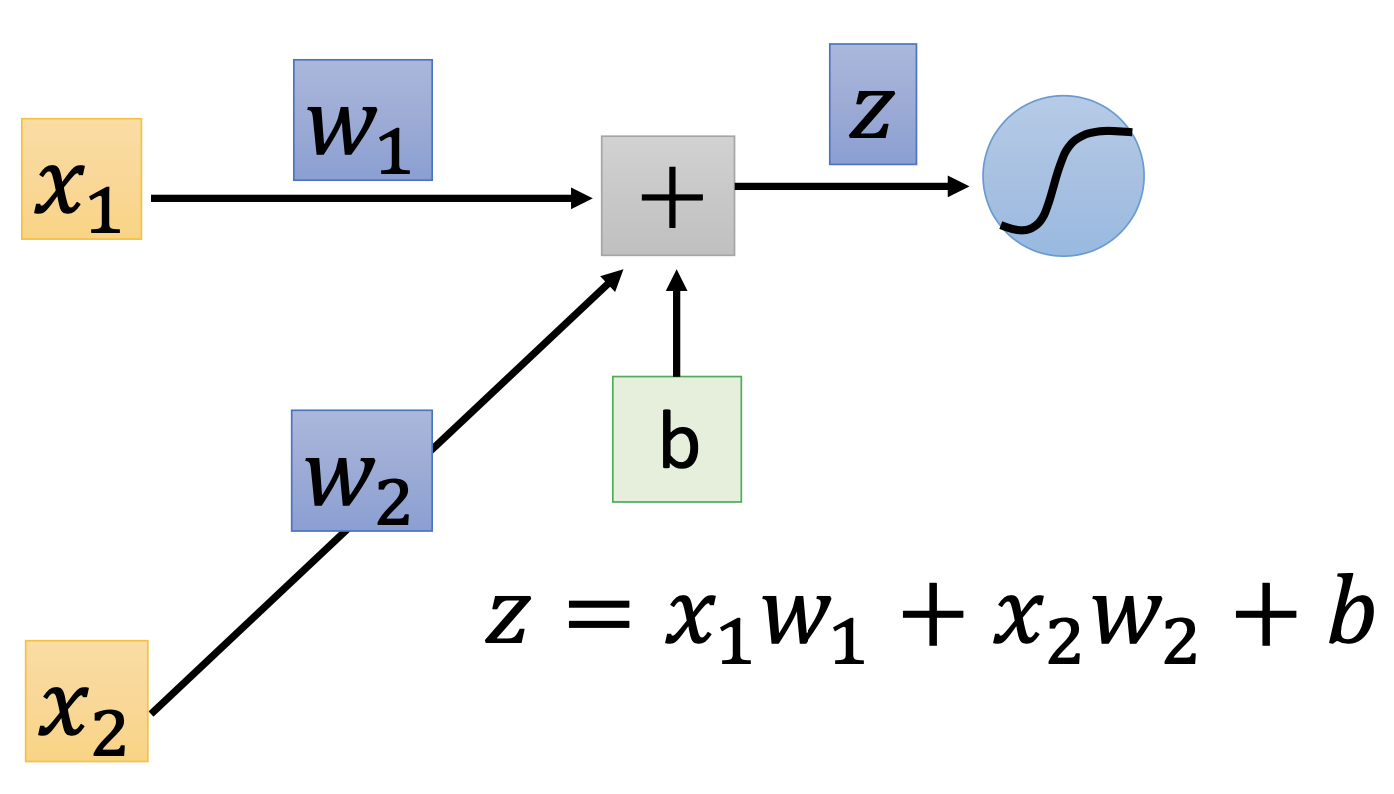
Then in forward pass, for all parameters, we compute
\[\frac{\partial z_p}{\partial w_i} = x_i\]for all parameters.
Backward Pass
In backward pass, we compute
\[\frac{\partial C^n}{\partial z_p} = \sigma'(z_p) \sum_{backward} w_j \frac{\partial C^n}{\partial z_k}\]where $w_j$ and $z_k$ pass backward to the node of $z_p$. For example
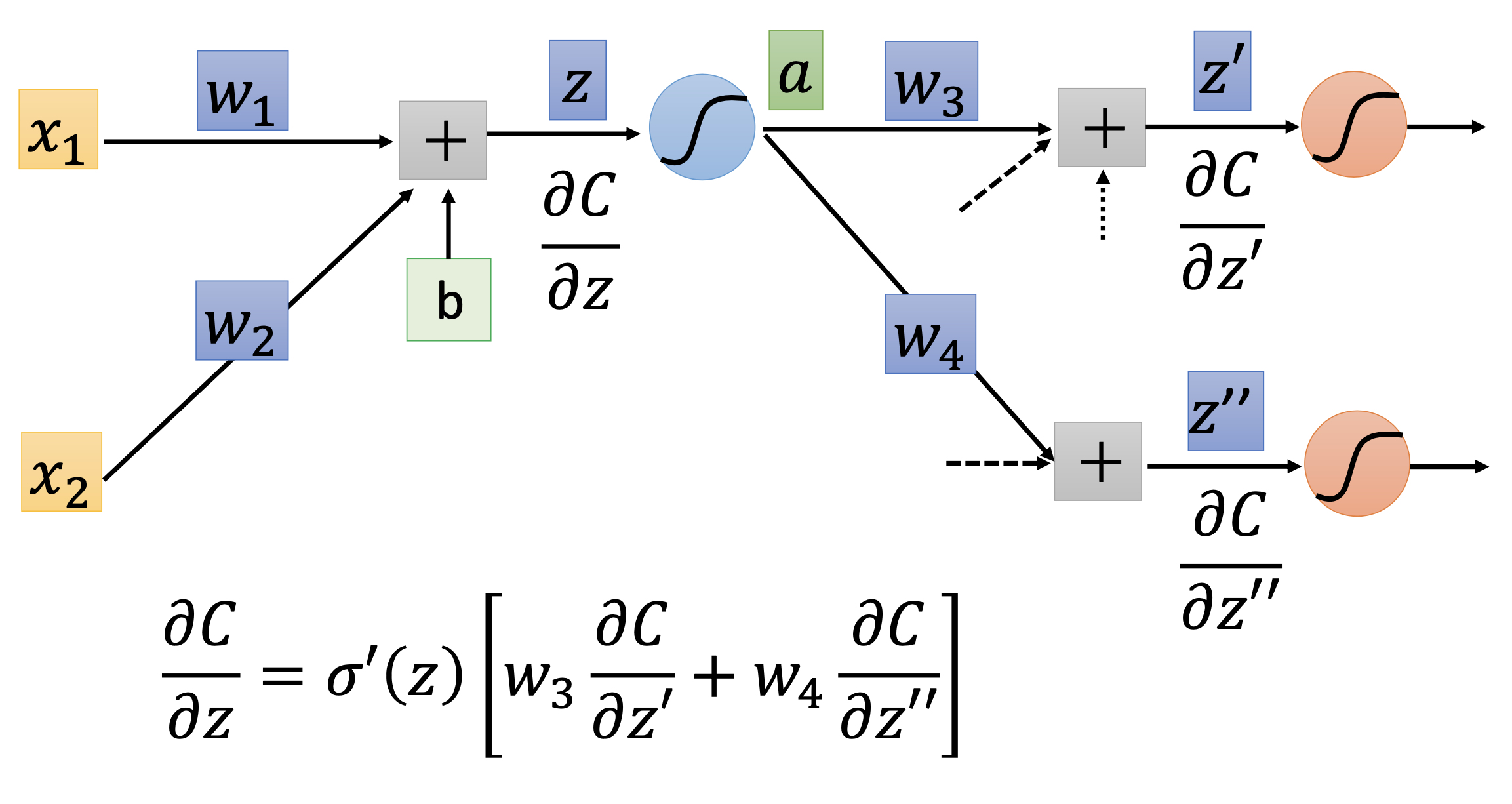
If a $z_k$ is at the output node, we can calculate $\frac{\partial C^n}{\partial z_k}$ directly by
\[\frac{\partial C^n}{\partial z_k} = \frac{\partial y_k}{\partial z_k} \frac{\partial C^n}{\partial y_k}\]and then pass backward to compute all the other $\frac{\partial C^n}{\partial z_k}$’s.
The concepts of forward and backward pass can be illustrated as