Notes for Prof. Hung-Yi Lee's ML Lecture 2, Sources of error.

July 10, 2021

Sources of error

• Bias
• Variance

Estimator

$\hat{f}$ is the theoretically best function. From training data, we find $f^*$ as an estimator of $\hat{f}$.

Bias & Viriance of Estimator

Assume the mean of variable $x$ is $\mu$ and the variance of variable $x$ is $\sigma^2$. To estimate the mean of $x$, the estimator of mean $\mu$:

\[m = \frac{1}{N}\sum_{n}x^{n} \neq \mu\]

while

\[E[m] = \frac{1}{N} \sum_{n} E[x^n] = \mu\]

$m$ is an unbiased estimator of $\mu$. and

\[Var[m] = \frac{\sigma^2}{N}\]

variance of $m$ depends on the number of samples.

Estimator of variance $\sigma^2$:

\[s^2 = \frac{1}{N}\sum_{n}(x^n - m)^2\]

while

\[E[s^2] = \frac{N-1}{N}\sigma^2 \neq \sigma^2\]

$s^2$ is a biased estimator of $\sigma^2$.

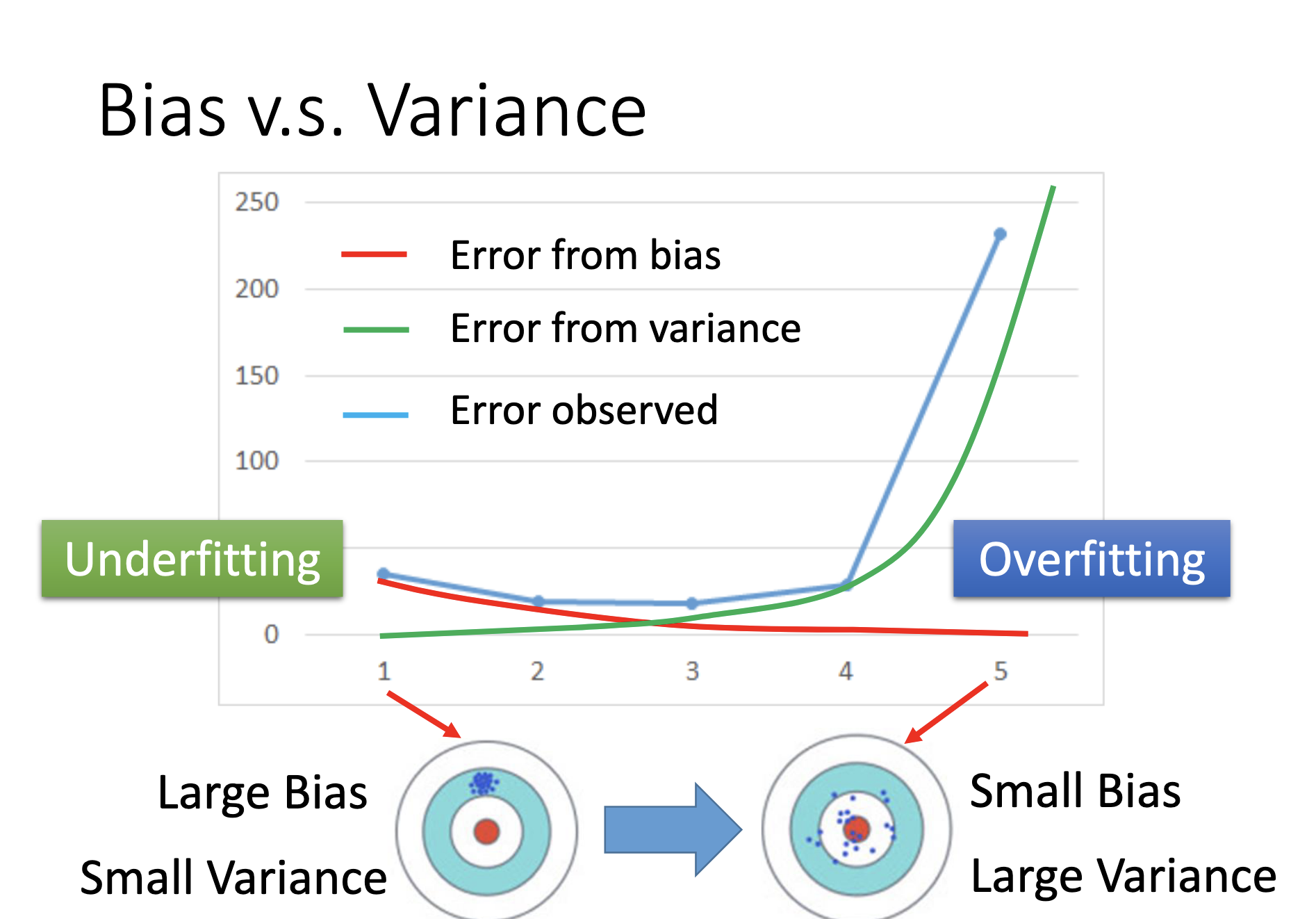
Bias v.s. Variance

Simple models may lead to small variances, large biases and underfitting. Complex model may lead to large variances, small biases and over fitting. An intuitive explaination:

• simple model => small function set => small variance & not large enough to cover the target => large bias
• complex model => large function set => large variance & high possibility to cover the target => small bias.

If the model can fit training data but can’t fit testing data, it’s overfitting and the error comes from variance. We should use more data or perform regularization.

If the model can’t fit the training data, it’s under fitting and the error comes from bias. We should ad more features as input or select a more complex model.

Model Selection

Threre ‘s usually trade-off between bias and variance, and we should select a model that balances two kinds of error to minimize the total error.

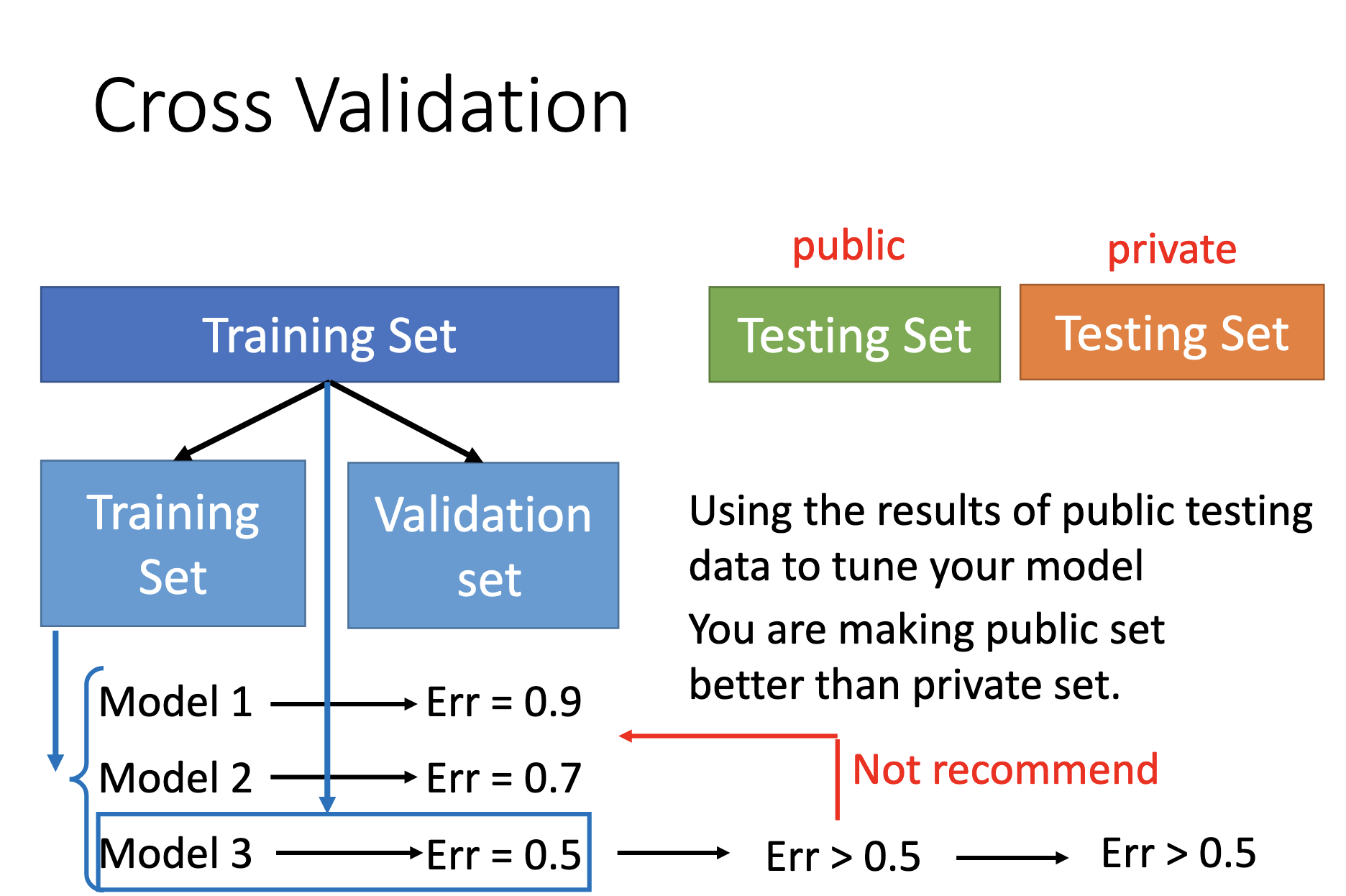
When choosing a model for a task, don’t train the models on the whole training set and select a model by the (public) testing set, because it’s highly possible to perform worse on the (real/private) testing set. Use (N-fold) cross validation instead.

Cross Validation

Procedures:

1. Separate the training set as 1 training set and 1 validation set.
2. Traing the models on the training set.
3. Evaluate the models on the validation set & select a model.
4. Re-train the selected model on the unseparated training set.
5. Use the trained model for the public & private testing set.

Also, don’t use the results of puclic testing set to tune the model; you’re making public testing set better that private testing set!

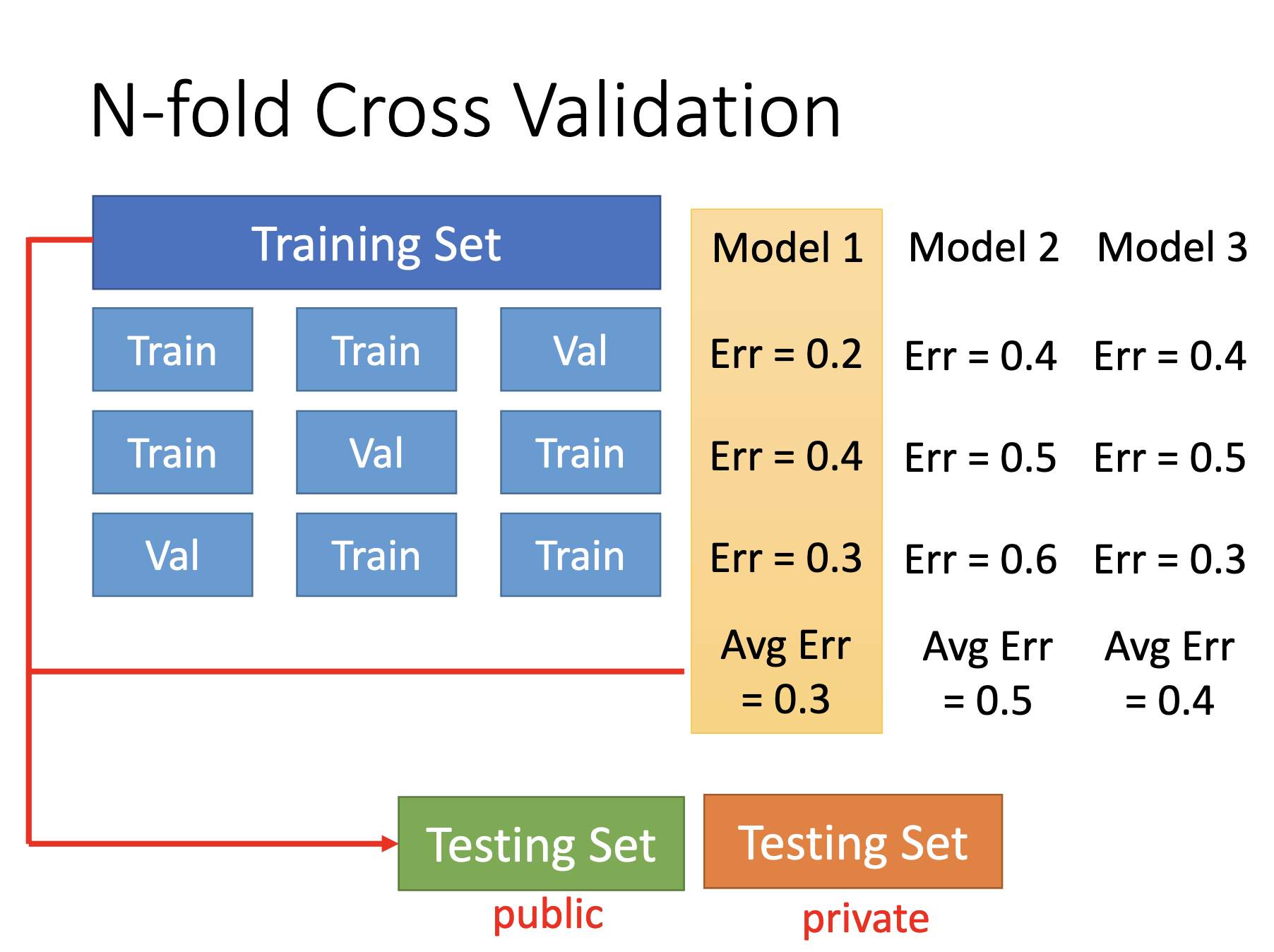
N-fold cross validation:

1. Separate the training set as N sets.
2. Choose 1 set as validation set and combine others as training set.
3. Train the models on the training set.
4. Evaluate the models on the validation set.
5. repeat 2~4 while N times while choosing every 1 set as the validation set once.
6. Select a model by the average of the performance in the repititions in step 5.
7. train the selected model by the whole original training set.
8. Use the trained model for the public & private testing set.

Reference

Youtube Link ML Lecture 2: Where does the error come from?

Course website

for the proof that $s^2$ is a bised estimator:

https://www.jamelsaadaoui.com/unbiased-estimator-for-population-variance-clearly-explained/

https://online.stat.psu.edu/stat415/lesson/1/1.3